Executive Assessment Table Analysis Questions
Table Analysis Question Type
Table Analysis (TA) questions present a table similar to a spreadsheet. The table can be sorted only in ascending order on any of its columns, by selecting the column's title from a drop-down menu given above the table. A brief text explaining the table is usually provided, and it is always important to read this information. The question presents three statements, values, or expressions. You may be asked whether each statement is true or false, or if "Yes" or "No" can be inferred from the information.
You may be asked to calculate mean, median, or range, calculate ratios, proportions, or probabilities, recognize correlations between two sets of data, compare data in relation to other data, or select a statement that best helps explain the data given in the prompt. Table Analysis prompts are interactive, and you are expected to be able to discern the most efficient way to sort the data to answer the question at hand.
Strategies and Concepts
As stated earlier, Table Analysis questions have you use an interactive table similar to a spread sheet, so you must gain experience working with Microsoft Excel tables. Table Analysis data are real-life data and thus they are often not round numbers. You can infer information from them using the listing property and sorting capability of these tables. However, in the EA-IR section, you can sort tables only in ascending order; you do not have the luxury of other Excel features, such as being able to calculate difference, ratio, mean, median, standard deviation, correlation factor, etc.
Commonly Tested Concepts in Table Analysis
Concepts commonly tested in Table Analysis are listed below. These include calculating the absolute difference between values, inferring through sorting, and finding mean, median, and mode. You will be asked to apply the concepts of measures of dispersion, as well as calculate absolute deviation, standard deviation, and range. We recommend you refer to the following list when studying for Table Analysis questions on the EA:
-
Calculate absolute deviation: in this case, you are looking for information about how much the data points deviate from the mean of the dataset.
-
Sort and infer: in this case you are sorting the information given in the table and inferring information from the data you are given.
-
Mean, Median, and Mode: these are relatively elementary math concepts; however, you will want to refresh yourself on these different statistical averages. The mean is what people generally think of as the average – in this case you add all of the data points together and divide them by the number of data points to find the average. The median is the middle value of all of the given data points. The mode is the value which occurs most often in the given data points.
-
Deviation: in this case, you are looking for the measure of difference between a value in the dataset and some other value, frequently the mean of the dataset.
-
Range: here you will be looking for the difference between the highest and lowest values in a dataset.
-
Standard Deviation: often the standard deviation is used to measure the spread of scores within a dataset. This is taking the statistics of an overall population and finding how some of the population deviate from the mean of the overall population.
-
Correlation: in this case, you will be asked to observe a linear relationship between two variables in the dataset. You will want to ask yourself, how does one variable seem to correspond with another variable?
Process of Solving TA Questions
-
Understand the dataset
Read the question narration, the table title, and the column headings of the table. Try to understand the relationship of one column with other column(s). Sometimes column headings are not very expressive; however, you can get information about them from the question narration or any note given outside the table area.
Don't be intimidated by the number of rows and number of columns. You will have to deal with only two to three columns and a few rows at a time. Quickly scan through the data given in the table. By doing this, you will grasp whether the data is given in integers or in decimal form. If the data is given in decimals, don't be intimidated. You can always approximate them to make manageable integers. -
Understand the question
As you know, there are three dichotomous statement type questions in a TA dataset. You have to mark each statement with either "Yes" or "No." Remember that there is no partial credit for correct response(s); each of the three responses must be correct for you to receive credit for the question.
Read the question statement and understand it. Rephrase the statement in your words, and if needed, translate it into mathematical language. -
Develop an approach
There could be two or more ways to approach a question. You may figure out that a question requires two-way sorting, but you can sort the table by one column at a time. So, figure out the best approach to solve the question. -
Apply the approach
Apply your approach to the question at hand and sort the table accordingly. You should jot down the results of any calculations you perform. It is likely that you might need one or two results from previous questions as intermediate steps for answering the questions that follow.
Example
The table presents quarterly sales and inventory data, in metric tons (MT), for Apex Corporation for a few steel products.
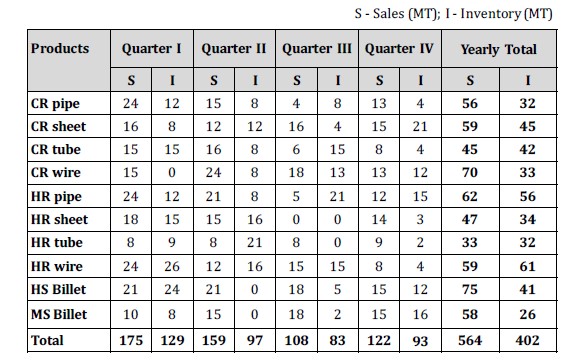
For each of the following statements, select "Yes" if the statement is true based on the information provided; otherwise select "No."

Solution, Part A
The question wants you to find out whether in the Q2, the deviation (difference) of CR tube sale from the Q2 arithmetic mean sale is less than that of other products.
In other words, the question statement states that for Q2, the sales of CR tube is closest to Q2 mean sales.
Mathematically, this means:
$| \text{CR tube sales} - \text{mean sales for Q2} | < | \text{Other products' sales} - \text{mean sales for Q2} |$
First, you calculate the mean sales for Q2.
Since
$\text{Total Q2 sales} =159 \text{ MT}$
and
$\text{Total number of products} = 10$
then
$\text{Q2 mean sales} = 159/10 = 15.9 \text{ MT}$
So,
$| \text{CR Tube sales} - \text{mean sales for Q2} | = | 16 - 15.9 | = 0.1$
Run through the values in column 4 (Q2 sales) and mentally deduct each value from 15.9. You will find that the deviation of CR Tube $\text{sales} = 0.1$ is the lowest among that of all the other products.
The answer for part A is "Yes."
Solution, Part B
The question wants you to find out whether in the Q4, the ratio of sales to inventory for HR~tubes is more than that for other products.
Mathematically, this means that for Q4,
$\left[\tfrac {\text{Sales}}{\text{Inventory}}\right]_{\text{HR tube}} > \left[\tfrac {\text{Sales}}{\text{Inventory}}\right]_{\text{Other products}} \Rightarrow \quad \left[\tfrac {\text{Sales}}{\text{Inventory}}\right]_{\text{HR tube}} = 9/2 = 4.5$
You have nine products for which you need to calculate the sales-to-inventory ratio, but that would be too time-consuming, and hence it is not advisable to compute.
A better approach would be to calculate a few select values. You know that for HR tubes, the value is 4.5, which is more than 1. You can skip the products for which sales are less than their inventory as the sales-to-inventory ratio value would be less than 1. Secondly, you can mentally divide sales by inventory to get probable contenders that have values, equalling more than 4. There is only one such product: HR sheets, which has a sales-to-inventory value equal to $14/3 = 4.67$, more than 4.5, so the statement is wrong.
The answer for part B is "No."
Solution, Part C
The question wants you to find out whether median sales for Q1 is more than median sales for each of Q2, Q3, and Q4.
Mathematically, this means:
$\mbox{Median sales} |_{\text{Q1}} > \mbox{Median sales} |_{\text{any other quarter}}$
To get the median sales of each quarter, sort the table by its sales columns to get the table:
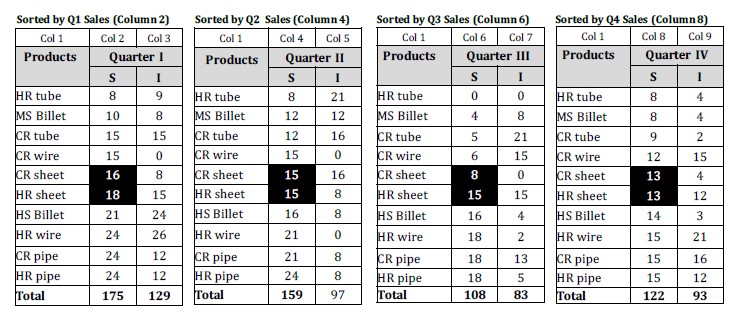
Median Sales for Q1:
$\text{Median of a series} = \mbox{value of the } \left(\tfrac {n+1}{2}\right)^\text{th} \text{ term}$
Here, median sales for Q1 equals:
$\mbox{Value of } \left(\tfrac {10+1}{2}\right)^\text{th} \text{ product} = \text{value of the } 5.5^\text{th} \text { product.}$
The value of the $5.5^\text{th}$ product equals
$\text{Average of 16 & 18} = (16+18)/2 = 17 \text{ MT}$
Similarly, median sales for Q2, Q3, and Q3 are (15 + 15)/2 = 15, (8 + 15)/2 = 11.5, and (13 + 13)/2 = 13 MT, respectively. Hence, the statement is correct.
The answer for the part C is "Yes."
